정렬(Sorting)
by Frinee이 글은 윤성우 저 - "윤성우의 열혈 자료구조"를 공부하고 정리하여 작성하였습니다.
1. 단순한 정렬 알고리즘
🫧 버블 정렬(Bubble Sort)
1. 이해와 구현
- 배열을 오름차순으로 정렬하는 과정

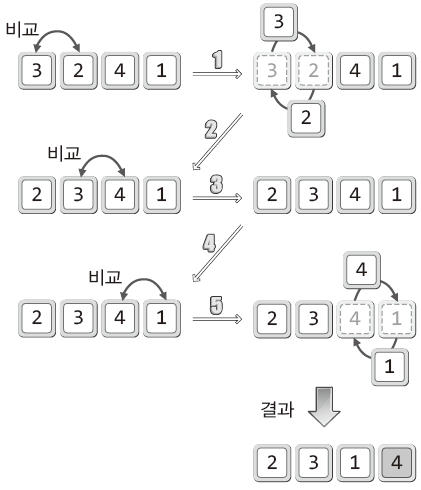
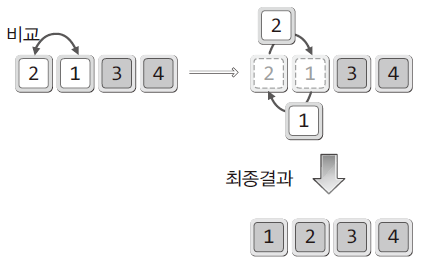
- 버블 정렬은 두 개의 데이터를 비교해가면서 정렬을 진행하는 방식
- 정렬의 우선순위가 가장 낮은 제일 큰 값을 맨 뒤로 보내는 방식
- 앞에서부터 순서대로 비교하고 교환하는 일련의 과정이 거품이 일어나는 모습에 비유되어 이름이 지어짐
- 🧑🏻💻 코드
void BubbleSort(int arr[], int n)
{
int i,j;
int temp;
for(i=0; i<n-1; i++)
{
for(j=0; j<(n-i)-1; j++)
{
if(arr[j] > arr[j+1])
{
// 데이터 교환
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}2. 성능평가
- 정렬 알고리즘의 평가의 근거는 다음 두 가지이다.
- 비교의 횟수: 두 데이터간의 비교연산의 횟수
- 이동의 횟수: 위치의 변경을 위한 데이터의 이동횟수
- 비교연산 횟수 : (n-1) + (n-2) + … + 2 + 1 = n^2 + …
- 이동연산 횟수: 정렬이 역순으로 된 상태면 비교연산 횟수 = 이동연산 횟수
- 시간 복잡도: O(n^2)
👈🏻 선택 정렬(Selection Sort)
1. 이해와 구현
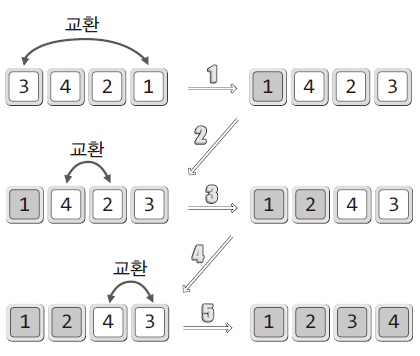
- 전자의 경우, 별도의 메모리 공간이 필요함.
- 후자처럼 개선하면 별도의 메모리 공간이 필요 없음
- 정렬 순서상 가장 앞서는 것을 선택해 가장 왼쪽으로 이동시키고 , 원래 그 자리에 있던 데이터는 빈 자리에 가져다 놓는 방식
- 🧑🏻💻 코드
void SelSort(int arr[], int n)
{
int i,j;
int maxIdx;
int temp;
for(i=0; i<n-1; i++)
{
maxIdx = i;
for(j=i+1; j<n; j++) // 최솟값 탐색
{
if(arr[j] < arr[maxIdx])
maxIdx = j;
}
// 데이터 교환
temp = arr[i];
arr[i] = arr[maxIdx];
arr[maxIdx] = temp;
}
}
}2. 성능평가
- 바깥쪽 for 문의 i 가 0일 때 안쪽 for 문의 j는 1~ n-1까지 증가하기 때문에 n-1회 연산 실행
- 비교연산 횟수: (n-1) + (n-2) + … + 2 + 1 = n^2 + … = O(n^2)
- 이동연산 횟수: 데이터 교환이 바깥쪽 for문에서 일어나기 때문에 O(n)
- 최악의 경우를 놓고 보면 버블 정렬보다 선택 정렬이 좋을 수 있지만 우열을 가리긴 힘들다.
📥 삽입 정렬(Insertion Sort)
1. 이해와 구현
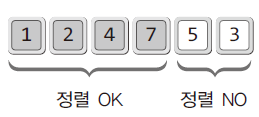
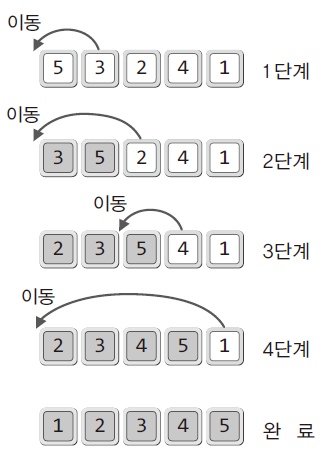
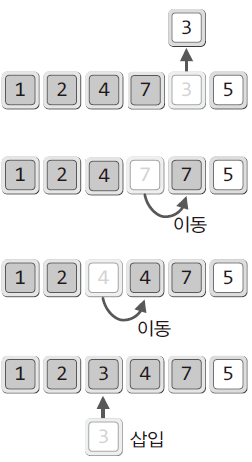
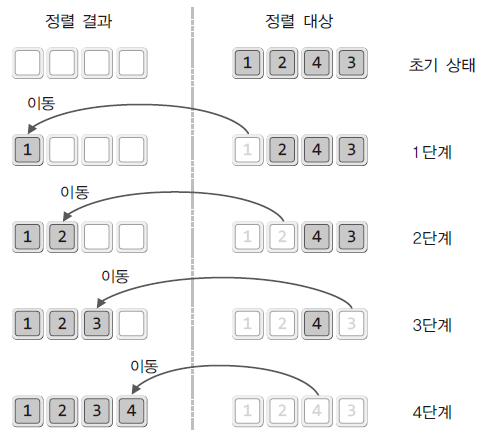
- 위 그림의 배열은 정렬이 완료된 부분과 완료되지 않은 부분으로 나뉨
- 정렬 대상을 두 부분으로 나눠 정렬 안 된 부분에 있는 데이터를 정렬된 부분의 특정 위치해 삽입해 가면서 정렬을 진행하는 알고리즘
- 🧑🏻💻 코드
void InsertSort(int arr[], int n) { int i,j; int insData; for(i=0; i<n; i++) { insData = arr[i]; // 정렬대상을 insData에 저장 for(j=i-1; j>=0; j--) { if(arr[j] > insData) arr[j+1] = arr[j]; // 비교대상 한 칸 뒤로 밀기 else break; // 삽입 위치 찾은 경우 탈출 } arr[j+1] = insData; // 찾은 위치에 정렬대상 삽입 } }
2. 성능평가
- 정렬 대상이 완전히 정렬된 상태이면 조건이 항상 거짓이 되어 break 문을 실행
- 최악의 경우는 버블정렬, 선택 정렬과 다르지 않고 항상 if 절의 true인 경우를 실행하여 이중 for문 만큼 비교와 이동연산이 실행
- 비교연산 횟수: O(n^2)
- 이동연산 횟수: O(n^2)
- 정확한 실행 횟수는 1부터 n-1까지의 등차수열의 합
2. 복잡하지만 효율적인 정렬 알고리즘
📚 힙 정렬(heap)
1. 이해와 구현
- 힙의 루트 노드에 저장된 값이 가장 커야 한다는 특성
- 힙의 루트 노드에 저장된 값이 정렬 순서상 가장 앞선다.
- 🧑🏻💻 코드
int PriComp(int n1, int n2) { return n2-n1; // 오름차순 정렬 // return n1-n2 // 내림차순 정렬 } void HeapSort(int arr[], int n, PriorityComp pc) { Heap heap; int i; HeapInit(&heap, pc); // 정렬대상을 가지고 힙을 구성한다. for(i=0; i<n; i++) HInsert(&heap, arr[i]); // 순서대로 하나씩 꺼내서 정렬을 완성 for(i=0; i<n; i++) arr[i] = HDelete(&heap); }
- 정렬 대상의 데이터들을 힙에 넣었다가 꺼내는 것이 전부
2. 성능평가
- 힙의 데이터 저장 시간 복잡도: O(logn)
- 힙의 데이터 삭제 시간 복잡도: O(logn)
- 정렬 대상의 수가 n 인 경우의 시간 복잡도: O(nlogn)
➕병합 정렬(Merge Sort)
1. 이해와 구현
- 병합 정렬은 “분할 정복” 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법
- ✂️ 분할 정복(divide and conpuer)
- 복잡한 문제를 복잡하지 않도록 분할하여 정복하는 방법
- 분할(divide): 해결이 용이한 단계까지 문제를 분할
- 정복(conquer): 해결이 용이한 수준까지 분할된 문제 해결
- 결합(combine): 분할해서 해결한 결과 결합하여 마무리
- 복잡한 문제를 복잡하지 않도록 분할하여 정복하는 방법
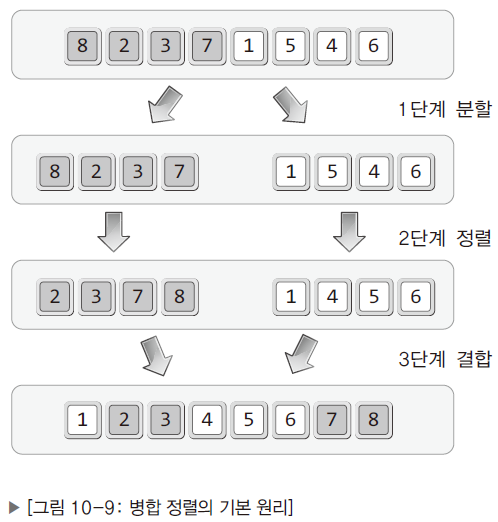
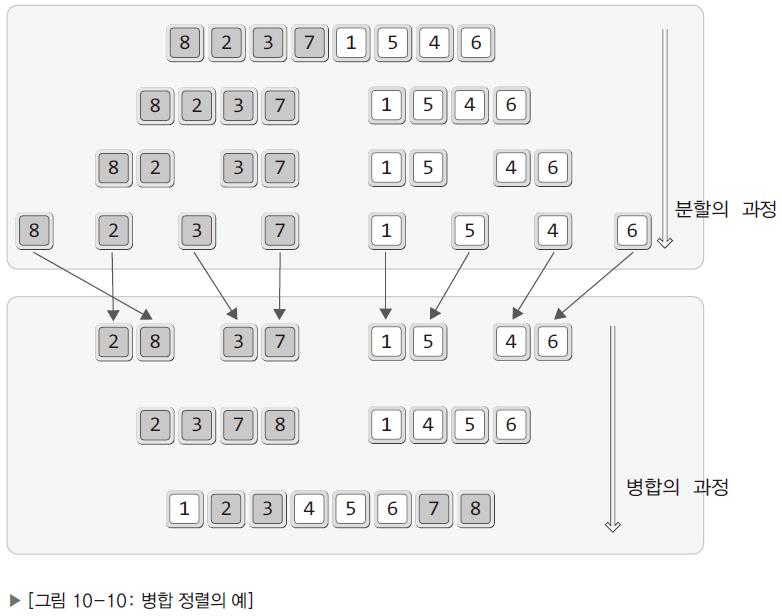
- 병합 정렬은 데이터가 1개만 남을 때까지 분할을 해나가고 데이터가 1개만 남는 경우, 정렬도 할 필요가 없어짐.
- 전체 데이터를 둘로 나누는 과정을 데이터가 하나씩 구분이 될 때까지 진행
- 분할을 완료한 후에는 정렬순서를 고려하여 둘을 하나로 묶는다.
- 재귀적인 구현을 위해 하나씩 구분이 될 때까지 둘로 나누는 과정을 반복
- MergeSort 함수 코드
void MergeSort(int arr[], int left, int right) { int mid; if(left < right) { mid = (left + right) / 2; MergeSort(arr, left, mid); MergeSort(arr, mid+1, right); // 정렬된 두 배열을 병합 MergeTwoArea(arr, left, mid, right) } }
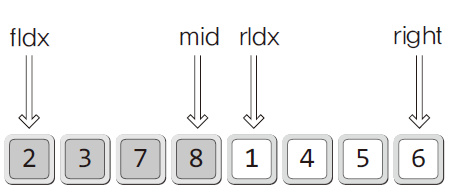
- left 와 right 는 정렬대상의 범위정보를 인덱스 값의 형태로 전달하는 역할
- MergeTwoArea 함수 코드
void MergeTwoArea(int arr[], int left, int mid, int right) { int fIdx = left; // 왼쪽 영역의 첫번째 위치 정보 int rIdx = right; // 오른쪽 영역의 첫번째 위치 정보 int i; int * sortArr = (int*)malloc(sizeof(int)*(right+1)); // 병합 결과를 담을 메모리 공간 할당 int sIdx = left; // 병합할 두 영역의 데이터들을 비교하여 // 정렬순서대로 sortArr에 하나씩 옮겨 담는다. // 두 영역 중 하나의 영역이라도 모두 다 담길 때까지 while(fIdx <= mid && rIdx <= right) { if(arr[fIdx] <= arr[rIdx]) sortArr[sIdx] = arr[fIdx++]; else sortArr[sIdx] = arr[rIdx++]; sIdx++; } // 앞 부분이 모두 sortArr로 갔다면 남은 뒷부분은 자동으로 sortArr 뒤로 다 처리 if(fIdx > mid) { for(i=rIdx; i <= right; i++, sIdx++) sortArr[sIdx] = arr[i]; } // 뒷 부분이 모두 sortArr로 갔다면 남은 앞부분은 자동으로 sortArr 뒤로 다 처리 else { for(i=fIdx; i <= mid; i++, sIdx++) sortArr[sIdx] = arr[i]; } // 병합결과를 옮겨 담기 for(i=left; i <= right; i++) arr[i] = sortArr[i]; free(sortArr); }

2. 성능평가
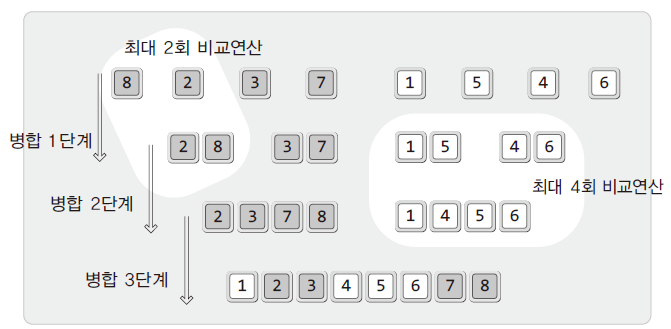
- 정렬의 우선순위를 비교하는 비교연산이 중심
- 정렬의 대상인 데이터 수가 n일 때, 각 병합단계마다 최대 n번의 비교연산이 진행
- 최대 비교연산 횟수: n(단계별 비교연산) x logn(병합 단계수) = nlogn = O(nlogn)
- 최대 이동연산 횟수
- 임시 배열에 데이터를 병합하는 과정에서 한 번 발생
- 임시 배열에 저장된 데이터 전부를 원위치하는 과정에서 한 번 발생
- 그러므로 비교연산 횟수의 2배인 2n*logn = O(nlogn)
💨퀵 정렬(Quick Sort)
1. 이해와 구현
- 퀵 정렬도 ‘분할 정복’에 근거하여 만들어진 정렬 방법
- 정렬대상을 반씩 줄여나가는 과정을 포함
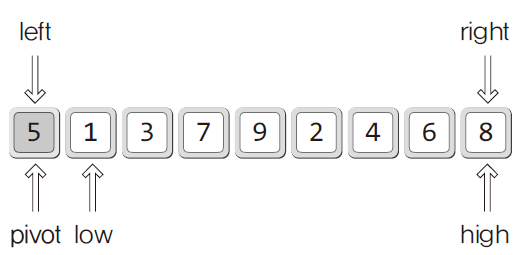
- left : 정렬대상의 가장 왼쪽 지점
- right: 정렬대상의 가장 오른쪽 지점
- pivot: 중심점, 중심축의 의미
- 가장 왼쪽에 위치한 데이터를 퀵 정렬에 필요한 피벗으로 정함
- high: 피벗을 제외한 가장 오른쪽에 위치한 지점
- low: 피벗을 제외한 가장 왼쪽에 위치한 지점
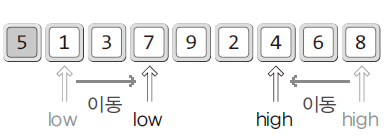
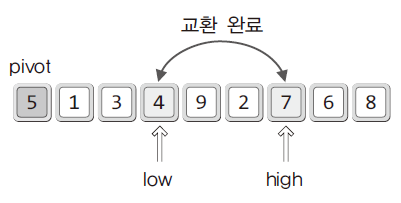
- 피벗보다 큰 값을 만날 때까지 low는 오른쪽으로 이동
- 피벗보다 작은 값을 만날 때까지 high는 왼쪽으로 이동
- 이동을 완료한 후에는 high와 low가 가리키는 데이터를 서로 교환함
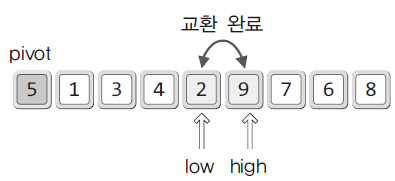
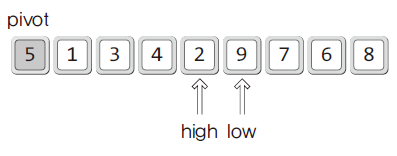
- 교환을 계속하다 보면 high와 low가 역전되는 상황이 발생함
- 이때에는 high와 pivot을 교환함.
- 마무리 했을 때, 피벗보다 작은 값들/피벗/피벗보다 큰 값들로 분류가 된 것을 알 수 있음
- 🧑🏻💻 코드
void Swap(int arr[], int idx1, int idx2)
{
int temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
int Partition(int arr[], int left, int right)
{
int pivot = arr[left]; // 피벗의 위치는 가장 왼쪽!
int low = left+1;
int high = right;
while(low <= high) // 교차되지 않을 때까지 반복
{
// 피벗보다 큰 값을 찾는 과정
while(pivot > arr[low])
low++; // low를 오른쪽으로 이동
// 피벗보다 작은 값을 찾는 과정
while(pivot < arr[high])
high--; // high를 왼쪽으로 이동
// 교차되지 않은 상태라면 Swap 실행
if(low <= high)
Swap(arr, low, high);
}
Swap(arr, left, high); // 피벗과 high가 가리키는 대상 교환
return high; // 옮겨진 피벗의 위치정보 반환
}
void QuickSort(int arr[], int left, int right)
{
if(left <= right)
{
int pivot = Partition(arr, left, right); // 둘로 나누고
QuickSort(arr, left, pivot-1); // 왼쪽 영역 정렬
QuickSort(arr, pivot+1, right); // 오른쪽 영역 정렬
}
}- 문제
- 만약 배열 안에 같은 값이 여러 개인 경우, 코드에 버그가 일어남
- 그래서 피벗과 low, high를 비교하는 로직의 수정이 필요함
// 피벗보다 크거나 같은 값을 찾고 맨 오른쪽 범위를 넘지 못하게
while(pivot >= arr[low] && low <= right)
low++;
// 피벗보다 작거나 같은 값을 찾고 pivot보다 왼쪽으로 가지 못하게
while(pivot <= arr[high] && hight >= (left+1))
high--;- pivot이 중간값에 해당하는 경우 가장 좋은 성능을 보임
- 반면, 정렬이 이미 된 경우, pivot이 제일 작은 값이므로 영역이 나뉘지 않고 새로운 pivot을 지정하여 다시 불필요하게 정렬하게 됨
- 그래서 정렬 대상에서 임의로 세 개의 데이터를 추출한 후, 중간 값을 pivot으로 선택하여 시작하기도 함.
2. 성능평가
- 하나의 피벗이 제자리를 찾아가는 과정은 배열 안의 데이터 수만큼인 n
- 영역이 정확히 같은 비율로 나뉘는 경우 둘로 나뉘는 횟수는 logn
- 최상의 퀵정렬의 비교연산 횟수: nlogn = O(nlogn)
- pivot이 잘못 설정되어 영역이 최악으로 나뉘는 경우 영역이 둘로 나뉘는 횟수는 n
- 최악의 퀵정렬 비교연산 횟수: n^2 = O(n^2)
- 하지만 퀵정렬은 실제로 평균적으로 최선에 가까운 O(nlogn)의 성능을 보여줌
- 별도의 메모리 공간도 소모하지 않기 때문에 동일한 빅-오 알고리즘 중 평균적으로 가장 빠른 정렬속도를 보임
🧮 기수 정렬(Radix Sort)
1. 이해 1
- 기수 정렬은 정렬순서상 앞서고 뒤섬의 판단을 위한 비교연산을 하지 않는 방법
- 정렬 알고리즘의 한계로 알려진 O(nlogn)을 뛰어 넘을 수 있음
- 길이가 같은 데이터들을 대상으로는 정렬이 가능하지만 그렇지 않은 경우 불가능함.
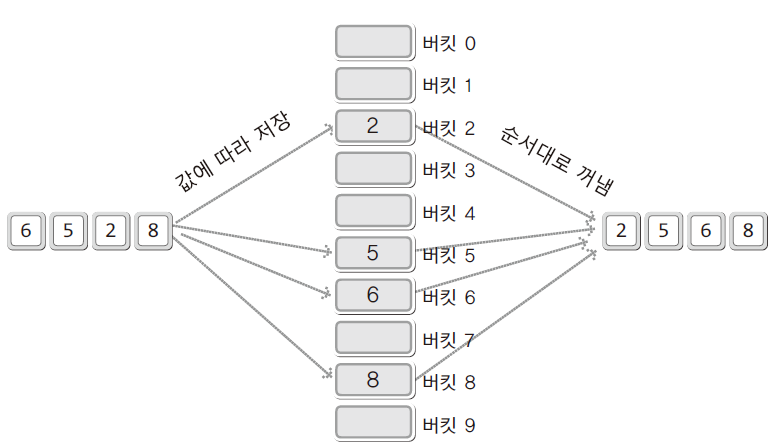
- 기수(radix)는 주어진 데이터를 구성하는 기본 요소를 뜻함
- 기수 정렬은 데이터를 구성하는 기본 요소, 즉 기수를 이용해서 정렬을 진행하는 방식
2. 이해 2
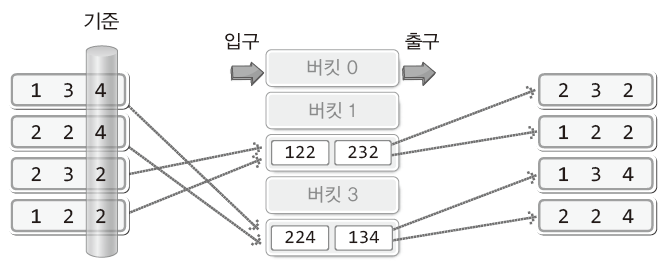
- ❓LSD 기수 정렬
- LSD(Least Significant Digit): 덜 중요한 자릿수
- 첫번째 자릿수 기준으로 버킷에 넣음
- 하나의 버킷에 둘 이상의 데이터가 존재하는 경우 들어간 순서대로 꺼냄
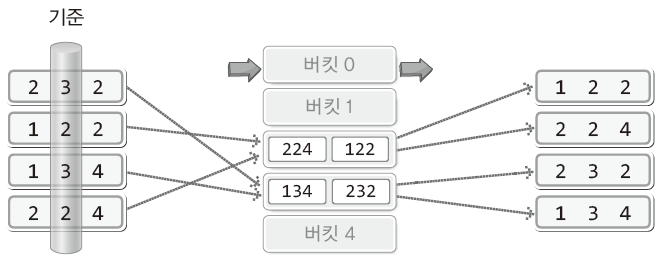
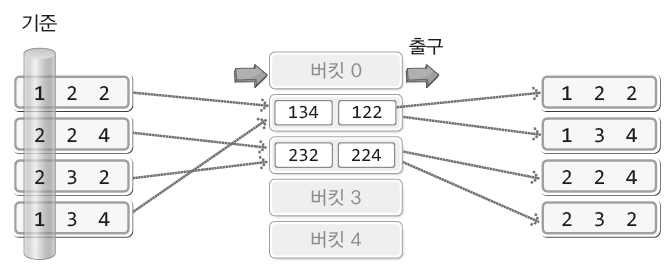
- 그 다음 두번째자릿수 기준으로 버킷에 넣음
- 해당 과정 반복하여 오름차순 정렬 완료
- 가장 중요한 자릿수를 비교해야 하기 때문에 모든 비교가 끝나야 값의 대소를 판단할 수 있음
- ❓MSD 기수 정렬
- MSD(Most Significant Digit): 가장 중요한 자릿수
- 가장 큰 자릿수 기준으로 버킷에 넣음
- 하지만 마지막까지 비교를 할 필요가 없고 중간에 정렬이 완료될 수 있음
- 대신에 MSD 방식에서는 중간에 데이터를 점검해야 하므로 성능이 반감될 수 있음
3. LSD 기준 구현
- LSD와 MSD의 빅-오는 동일함
- MSD의 경우 정렬의 과정이 단축될 수 있지만 모든 데이터에 일괄적인 과정을 거쳐야 하기 때문에 추가 연산과 별도의 메모리가 필요함
- 🧑🏻💻 코드
void RadixSort(int arr[], int num, int maxLen) { // 매개변수 maxLen은 정렬대상 중 가장 긴 데이터 길이 정보 Queue buckets[BUCKET_NUM]; int bi; int pos; int di; int divfac = 1; int radix; // 총 10개의 버킷 초기화 for(bi=0; bi<BUCKET_NUM; bi++) QueueInit(&buckets[bi]); // 가장 긴 데이터의 길이만큼 반복 for(pos=0; pos<maxLen; pos++) { // 정렬대상의 수만큼 반복 for(di=0; di<num; di++) { // N번째 자리의 숫자 추출 radix = (arr[di]/ divfac) % 10; // 추출한 숫자 근거로 버킷에 저장 Enqueue(&buckets[radix], arr[di]); } // 버킷 수만큼 반복 for(bi=0, di=0; bi<BUCKET_NUM; bi++) { // 버킷에 저장된 것 순서대로 다 꺼내서 다시 arr에 저장 while(!QIsEmpty(&buckets[bi])) arr[di++] = Dequeue(&buckets[bi]); } // N번째 자리의 숫자 추출을 위한 피제수의 증가 divfac *= 10; } }
4. 성능평가
- 기수 정렬의 시간 복잡도는 삽입과 추출 빈도수를 대상으로 결정
- 버킷을 대상으로 하는 데이터의 삽입과 추출을 한 쌍의 연산으로 볼 때 한 쌍의 연산 수행 횟수는 maxLen x num
- 정렬대상의 수가 n이고, 정렬대상의 길이가 l일 때 시간 복잡도는 O(ln)
자료
- 윤성우의 열혈 자료구조 (윤성우 저, 2023.10)
'[컴퓨터 과학자 스터디] > 자료구조' 카테고리의 다른 글
| 탐색(Search) 2 (0) | 2024.12.02 |
|---|---|
| 탐색(Search) 1 (1) | 2024.12.02 |
| 우선순위 큐(Priority Queue)와 힙(Heap) (0) | 2024.11.24 |
| 트리(tree) (0) | 2024.11.23 |
| 큐(queue) (0) | 2024.11.21 |
블로그의 정보
프리니의 코드저장소
Frinee