탐색(Search) 1
by Frinee이 글은 윤성우 저 - "윤성우의 열혈 자료구조"를 공부하고 정리하여 작성하였습니다.
1. 탐색의 이해와 보간 탐색
❓ 탐색의 이해
- 데이터를 찾는 방법을 말함.
- 효율적인 탐색은 대부분 트리의 연장성상에서 이루어짐.
🚨 보간 탐색(interpolation Search)
- 보간 탐색은 이진 탐색의 비효율성을 개선시킨 알고리즘이다.
- 보간 탐색은 이진 탐색과 마찬가지로 모두 정렬이 완료된 데이터를 대상으로 진행함.
“이진 탐색처럼 그냥 중앙에서 시작하지 말고, 탐색대상이 앞쪽에 위치해 있으면 앞쪽에서 탐색을 시작하자!”



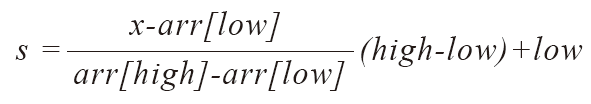
- 비례식을 구성하여 탐색 위치의 인덱스 값을 계산한다.
- 다만 오차율을 최소화하기 위해 실수형 나눗셈을 진행한다.
🔑 탐색 키(Search Key)와 탐색 데이터(Search Data)
typedef int Key; // 탐색 키에 대한 typedef 선언
typedef double Data; // 탐색 데이터에 대한 typedef 선언
typedef struct item
{
Key searchKey; // 탐색 키(search key)
Data searchData; // 탐색 데이터(search data)
} Item;
🧑🏻💻 보간 탐색의 구현
int ISearch(int ar[], int first, int last, int target)
{
int mid;
if(ar[first] > target || ar[last] < target)
return -1; // 탐색 실패
// 이진 탐색과의 차이점
mid = ((double)(target - ar[first]) / (ar[last] - ar[first]) * (last - first)) + first;
if(ar[mid] == target)
return mid;
else if(target < ar[mid])
return ISearch(ar, first, mid-1, target);
else
return ISearch(ar, mid+1, last, target);
}
⚠️ 탈출조건을 만족하지 않는 이유
ex)
int arr\[\] = {1,3,5,7,9};
ISearch(arr,1,4,2);
mid = 0 이 저장됨.
- 그래서
return ISearch(ar, mid+1, last, target)이 실행이 되버리고 이는ISearch(arr, 1, 4, 2)가 되어 탈출할 수 없음 - 그래서
if(ar\[first\] > target || ar\[last\] < target) return -1;// 탐색 실패를 설정해준다.
2. 이진 탐색 트리
- 이진 트리에 데이터 저장 규칙을 더해 놓은 것이 이진 탐색 트리라 할 수 있다.
- 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
- 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
왼쪽 자식 노드의 키 < 부모 노드의 키 < 오른쪽 자식 노드의 키
- 이진 탐색 트리에 데이터를 추가한다 했을 때
- 루트 노드와 비교했을 때, 값이 크면 오른쪽 자식 노드로 이동
- 루트 노드와 비교했을 때, 값이 작으면 왼쪽 자식 노드로 이동
- 왼쪽/오른쪽 노드가 없으면 그 위치에 저장
🌲 이진 탐색 트리 헤더 파일
- BinaryTree2.h
BTreeNode * MakeBTreeNode(void);
- 노드를 동적으로 할당해서 그 노드의 주소 값을 반환한다.
BTData GetData(BTreeNode * bt);
- 노드에 저장된 데이터를 반환한다.
void SetData(BTreeNode *bt, BTData data);
- 인자로 전달된 데이터를 노드에 저장한다.
BTreeNode * GetLeftSubTree(BTreeNode * bt);
- 인자로 전달된 노드의 왼쪽 자식 노드의 주소 값을 반환
BTreeNode * GetRightSubTree(BTreeNode * bt);
- 인자로 전달된 노드의 오른쪽 자식 노드의 주소 값을 반환
void MakeLeftSubTree(BTreeNode *main, BTreeNode *sub);
- 인자로 전달된 노드의 왼쪽 자식 노드를 교체
void MakeRightSubTree(BTreeNode *main, BTreeNode *sub);
- 인자로 전달된 노드의 오른쪽 자식 노드를 교체- BinarySearchTree.h
#include "BinaryTree2.h"
typedef BTData BSTData;
// BST의 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode *bst);
// BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
// BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode *bst, BSTData target);
🌳 이진 탐색 트리: 삽입과 탐색
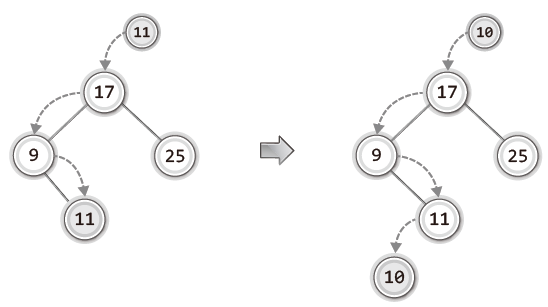
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL; // parent Node
BTreeNode * cNode = *pRoot; // current Node
BTreeNode * nNode = NULL; // new Node
// 새로운 노드가 추가될 위치를 찾는다.
while(cNode != NULL)
{
if(data == GetData(cNode))
return; // 키의 중복 허용하지 않음
pNode = cNode;
if(GetData(cNode) > data)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
//pNode의 자식노드로 추가할 새 노드의 생성
nNode = MakeBTreeNode(); // 새 노드 생성
SetData(nNode, data); // 새 노드에 데이터 저장
//pNode의 자식 노드로 새 노드를 추가
if(pNode != NULL) // 새 노드가 루트 노드가 아니라면,
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else
{
*pRoot = nNode;
}
}
BTreeNode * BSTSearch(BTreeNode *bst, BSTData target)
{
BTreeNode * cNode = bst; // current node
BSTData cd; // current data
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target < cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL;
}
🌳❌ 이진 탐색 트리: 삭제
- 이진 탐색 트리에서 임의의 노드를 삭제하는 경우, 삭제 후에도 이진 탐색 트리가 유지되도록 빈 자리를 채워야 함.
- 상황 1 : 삭제할 노드가 단말 노드인 경우

if(삭제할 노드가 단말 노드이면)
{
if(GetLeftSubTree(pNode) == dNode) // 삭제할 노드가 왼쪽 자식 노드라면
RemoveLeftSubTree(pNode);
else
RemoveRightSubTree(pNode);
}
- 상황 2: 삭제할 노드가 하나의 자식 노드를 갖는 경우

if(삭제할 노드가 하나의 자식 노드를 갖고 있다면)
{
BTreeNode * dcNode;
// 삭제 대상의 자식 노드를 찾는다.
if(GetLeftSubTree(dNode) != NULL) // 자식 노드가 왼쪽이라면
dcNode = GetLeftSubTree(dNode);
else
dcNode = GetRightSubTree(dNode);
// 삭제 대상의 부모 노드와 자식 노드를 연결한다.
if(GetLeftSubTree(pNode) == dNode) // 삭제 대상이 왼쪽 자식 노드이면
ChangeLeftSubTree(pNode, dcNode); // 왼쪽 연결
else
ChangeRightSubTree(pNode, dcNode);
}
- 상황 3: 삭제할 노드가 두 개의 자식 노드를 갖는 경우


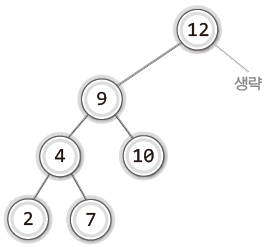
- 왼쪽 서브트리의 가장 큰 값, 또는 오른쪽 서브트리의 가장 작은 값으로 대체한다.

- 가장 큰 값을 찾을 때는 NULL을 만날 때까지 계속 오른쪽 자식 노드로 이동
- 가장 작은 값을 찾을 때는 NULL을 만날 때까지 계속해서 왼쪽 자식 노드로 이동
“삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 지니는 노드를 찾아서 이것으로 삭제할 노드를 대체한다.”
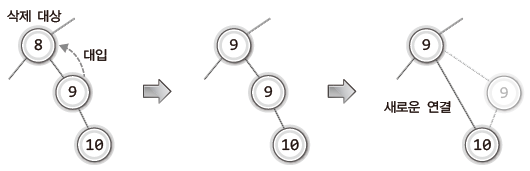
- 단계 1 : 삭제할 노드를 대체할 노드를 찾는다.
- 단계 2 : 대체할 노드에 저장된 값을 삭제할 노드에 대입한다.
- 단계 3 : 대체할 노드의 부모 노드와 자식 노드를 연결한다.
if(삭제할 노드가 두 개의 자식 노드를 지닌다.)
{
BTreeNode * mNode = GetRightSubTree(dNode); // 대체 노드
BTreeNode * mpNode = dNode; // 대체 노드의 부모 노드
// 단계 1. 삭제 대상의 대체 노드를 찾는다.
while(GetLeftSubTree(mNode) != NULL)
{
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
// 단계 2. 대체할 노드에 저장된 값을 삭제할 노드에 대입한다.
SetData(dNode, GetData(mNode));
// 단계 3. 대체할 노드의 부모 노드와 자식 노드를 연결한다.
if(GetLeftSubTree(mpNode) == mNode)
{
// 대체할 노드의 자식 노드를 부모 노드의 왼쪽에 연결
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
}
else
{
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
}
}
🎄❌ 이진 탐색 트리: 삭제를 위한 이진 트리 확장
// 왼쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값이 반환된다.
BTreeNode * RemoveLeftSubTree(BTreeNode *bt)
{
BTreeNode * delNode;
if(bt != NULL){
delNode = bt->left;
bt->left = NULL;
}
return delNode;
}
// 오른쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값이 반환된다.
BTreeNode * RemoveRightSubTree(BTreeNode *bt)
{
BTreeNode * delNode;
if(bt != NULL){
delNode = bt->right;
bt->right = NULL;
}
return delNode;
}
// 메모리 소멸을 수반하지 않고 main의 왼쪽 자식 노드를 변경
void ChangeLeftSubTree(BTreeNode *main, BTreeNode * sub)
{
main->left = sub;
}
// 메모리 소멸을 수반하지 않고 main의 오른쪽 자식 노드를 변경
void ChangeRightSubTree(BTreeNode *main, BTreeNode * sub)
{
main->right = sub;
}
🎄이진 탐색 트리: 완전한 구현 🎄
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target)
{
BTreeNode *pVRoot = MakeBTreeNode();
BTreeNode *pNode = pVRoot;
BTreeNode *cNode = *pRoot;
BTreeNode *dNode;
// 루트 노드를 pVRoot가 가리키는 노드의 오른쪽 자식 노드가 되게 한다.
ChangeRightSubTree(pVRoot, *pRoot);
// 삭제 대상인 노드를 탐색
while(cNode != NULL && GetData(cNode) != target)
{
pNode = cNode;
if(target < GetData(cNode))
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
if(cNode == NULL)
return NULL;
dNode = cNode;
// 1. 삭제할 노드가 단말 노드이면
if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL)
{
if(GetLeftSubTree(pNode) == dNode) // 삭제할 노드가 왼쪽 자식 노드라면
RemoveLeftSubTree(pNode);
else
RemoveRightSubTree(pNode);
}
// 2. 삭제할 노드가 하나의 자식 노드를 갖고 있다면
else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL)
{
BTreeNode * dcNode;
// 삭제 대상의 자식 노드를 찾는다.
if(GetLeftSubTree(dNode) != NULL) // 자식 노드가 왼쪽이라면
dcNode = GetLeftSubTree(dNode);
else
dcNode = GetRightSubTree(dNode);
// 삭제 대상의 부모 노드와 자식 노드를 연결한다.
if(GetLeftSubTree(pNode) == dNode) // 삭제 대상이 왼쪽 자식 노드이면
ChangeLeftSubTree(pNode, dcNode); // 왼쪽 연결
else
ChangeRightSubTree(pNode, dcNode);
}
// 3. 삭제할 노드가 두 개의 자식 노드를 지닌다.
else
{
BTreeNode * mNode = GetRightSubTree(dNode); // 대체 노드
BTreeNode * mpNode = dNode; // 대체 노드의 부모 노드
int delData;
// 단계 1. 삭제 대상의 대체 노드를 찾는다.
while(GetLeftSubTree(mNode) != NULL)
{
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
// 단계 2. 대체할 노드에 저장된 값을 삭제할 노드에 대입한다.
delData = GetData(dNode); // 대입 전 데이터 백업
SetData(dNode, GetData(mNode));
// 단계 3. 대체할 노드의 부모 노드와 자식 노드를 연결한다.
if(GetLeftSubTree(mpNode) == mNode)
// 대체할 노드의 자식 노드를 부모 노드의 왼쪽에 연결
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
else
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
dNode = mNode;
SetData(dNode, delData);
}
// 삭제된 노드가 루트노드라면
if(GetRightSubTree(pVRoot) != *pRoot)
*pRoot = GetRightSubTree(pVRoot); // 루트 노드 변경
free(pVRoot); // 가상 루트 노드 소멸
return dNode;
}

- 가상 루트 노드를 둔 이유는 삭제할 노드가 루트 노드인 경우를 일반화하기 위함.
자료
- 윤성우의 열혈 자료구조 (윤성우 저, 2023.10)
'[컴퓨터 과학자 스터디] > 자료구조' 카테고리의 다른 글
| 테이블(Table)과 해쉬(Hash) (2) | 2024.12.05 |
|---|---|
| 탐색(Search) 2 (0) | 2024.12.02 |
| 정렬(Sorting) (0) | 2024.11.27 |
| 우선순위 큐(Priority Queue)와 힙(Heap) (0) | 2024.11.24 |
| 트리(tree) (0) | 2024.11.23 |
블로그의 정보
프리니의 코드저장소
Frinee