그래프(Graph)
by Frinee이 글은 윤성우 저 - "윤성우의 열혈 자료구조"를 공부하고 정리하여 작성하였습니다.
1. 그래프의 이해와 종류
그래프 이해와 종류


- 연결 관계에 있어 방향성이 없는 그래프를 무방향 그래프라 함.
- 간선에 방향 정보가 포함된 그래프를 방향 그래프라 함.
- 완전 그래프(complete graph): 각각의 정점에서 다른 모든 정점을 연결한 그래프


가중치 그래프(weight graph)와 부분 그래프(Sub graph)


- 가중치는 두 정점 사이의 거리나 소요 시간 같은 정보가 될 수 있음.
- 부분 그래프는 원 그래프의 일부 정점 및 간선으로 이뤄진 그래프를 뜻함.
그래프의 집합 표현




- 그래프 G의 정점 집합 → V(G)
- 그래프 G의 간선 집합 → E(G)
V(G1) = {A, B, C, D}, E(G1) = {(A,B), (A,C), (A,D), (B,C), (C,D)}V(G2) = {A, B, C, D}, E(G2) = {(A,C), (A,D), (B,C)}V(G3) = {A, B, C, D}, E(G3) = {<A,B>, <A,C>, <D,A>}V(G4) = {A, B, C, D}, E(G4) = {<A,C>, <B,C>, <D,A>}
그래프의 ADT
void GraphInit(UALGraph *pg, int nv);
- 그래프의 초기화를 진행
- 두 번째 인자로 정점의 수를 전달
void GraphDestroy(UALGraph *pg);
- 그래프 초기화 과정에서 할당한 리소스를 반환
void AddEdge(UALGraph *pg, int fromV, int toV);
- 매개변수 fromV와 toV로 전달된 정점을 연결하는 간선을 그래프에 추가
void ShowGraphEdgeInfo(UALGraph *pg);
- 그래프의 간선 정보를 출력
그래프 구현 방법
- 인접 행렬 기반 그래프 → 정방 행렬을 활용
- 인접 리스트 기반 그래프 → 연결 리스트 활용

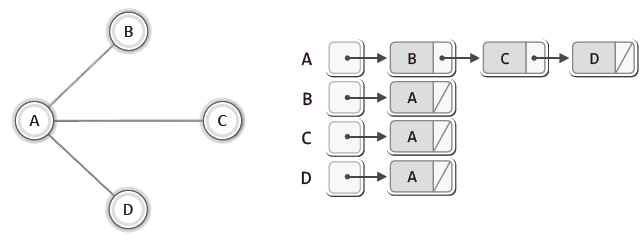
2. 인접 리스트 기반의 그래프 구현
헤더파일 정의
typedef struct _ual
{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
}
// 그래프 초기화
void GraphInit(UALGraph *pg, int nv);
// 그래프 리소스 해제
void GraphDestroy(UALGraph *pg);
// 간선의 추가
void AddEdge(UALGraph *pg, int fromV, int toV);
// 간선의 정보 출력
void ShowGraphEdgeInfo(UALGraph *pg);
그래프 구현
- GraphInit
void GraphInit(ALGraph *pg, int nv)
{
int i;
// 정점의 수에 해당하는 길이의 리스트 배열을 생성
pg-> adjList = (List*)malloc(sizeof(List)*nv); // 간선정보를 저장할 리스트 생성
pg->numV = nv; // 정점의 수는 nv에 저장된 값으로 결정
pg->numE = 0; // 초기 간선 수는 0
// 정점의 수만큼 생성된 리스트들을 초기화
for(i=0; i<nv; i++)
{
ListInit(&(pg->adjList[i]));
SetSortRule(&(pg->adjList[i]), WhoIsPrecede); // 리스트의 정렬기준 설정
}
}- GraphDestroy
void GraphDestroy(ALGraph * pg)
{
if(pg->adjList != NULL)
free(pq->adjList); // 동적으로 할당된 연결 리스트 소멸
}- AddEdge
void AddEdge(ALGraph *pg, int fromV, int toV)
{
// 정점 fromV의 연결 리스트에 정점 toV의 정보 추가
LInsert(&(pg->adjList[fromV]), toV);
// 정점 toV의 연결 리스트에 정점 fromV 정보 추가
LInsert(&(pg->adjList[toV], fromV);
pg->numE += 1;
}3. 그래프의 탐색
깊이 우선 탐색(DFS)

- DFS의 핵심 ex) 비상연락망
- 한 사람에게만 연락을 한다.
- 연락할 사람이 없으면, 자신에게 연락한 사람에게 이를 알린다.
- 처음 연락을 시작한 사람의 위치에서 연락은 끝이 난다.
너비 우선 탐색(BFS)




- 한 사람을 기준으로 연결된 모든 사람에게 메시지를 전달하는 방식
DFS 구현

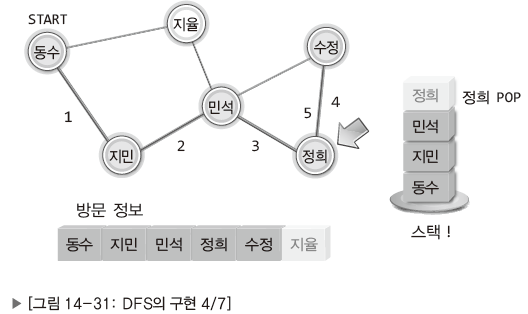
- 스택: 경로 정보의 추적을 목적으로 활용
- 배열: 방문 정보의 기록을 목적으로 활용
- 방문할 정점을 떠날 때, 떠나는 정점의 정보를 스택에 쌓는다.
- 만약 연결된 노드 중 방문하지 않은 곳이 없다면 스택에서 꺼내어 확인한다.
- 연결된 노드 중 방문하지 않은 곳이 존재할 때까지 스택에서 꺼낸다.
- 모든 노드를 다 방문한 경우, 시작점으로 돌아간다.
BFS 구현
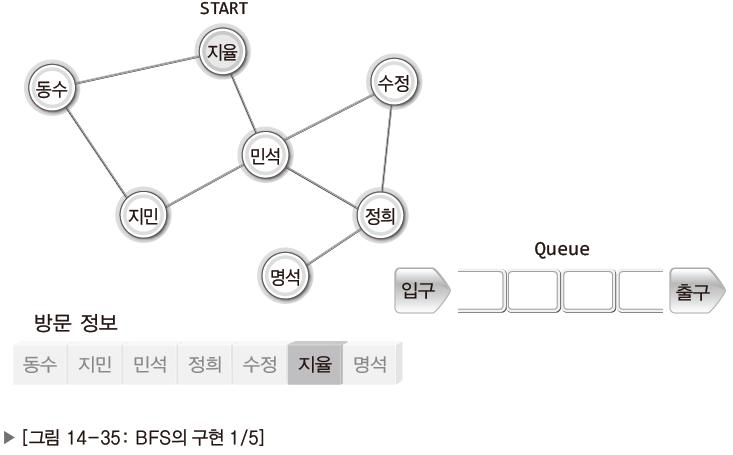

- 큐: 방문 차례의 기록을 목적으로 함.
- 배열: 방문 정보의 기록을 목적으로 함.
- 연결된 인접 노드의 정보가 큐에 순서대로 들어감.
- 큐에서 하나 꺼내어 해당 노드와 인접한 노드를 찾고 그 중 방문하지 않은 노드를 다시 큐에 넣는다.
- 방문하지 않은 노드가 없을 때까지 1,2를 반복함.
4. 최소 비용 신장 트리
사이클을 형성하지 않는 그래프


- 두 개의 정점을 잇는 간선을 경로라 함.
- 그 중 동일한 간선을 중복하여 포함하지 않는 경로를 단순 경로라 함.
- 단순 경로이면서 시작과 끝이 같은 경로를 사이클(cycle)이라 함.
최소 비용 신장 트리의 이해와 적용
- 신장 트리의 특징
- 그래프의 모든 정점이 간선에 의해서 하나로 연결되어 있다.
- 그래프 내에서 사이클을 형성하지 않음
- 신장 트리의 모든 간선의 가중치 합이 최소인 그래프를 최소 비용 신장 트리(MST, minimum cost spanning tree)라 함.


최소 비용 신장 트리의 구성을 위한 크루스칼 알고리즘
- 크루스칼(Kruskal) 알고리즘
- 가중치를 기준으로 간선을 정렬한 후에 MST가 될 때까지 간선을 하나씩 선택 또는 삭제해 나가는 방식
- 프림(Prim) 알고리즘
- 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장해 나가는 방식

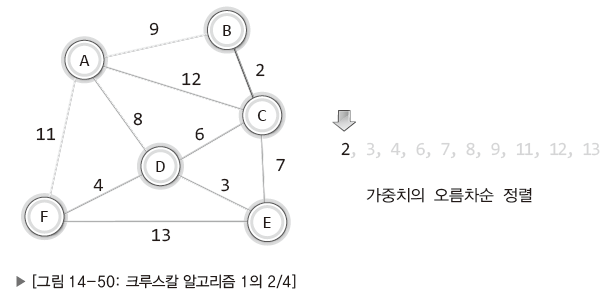


- 크루스칼 알고리즘의 핵심
- 가중치를 기준으로 간선을 오름차순 정렬
- 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가
- 사이클을 형성하는 간선은 추가하지 않음
- 간선의 수가 정점의 수보다 하나 적을 때 MST 완성
- 반대로 간선을 내림차순 정렬하고 하나씩 소거하는 방법도 존재함.
- 이 때의 크루스칼 알고리즘 핵심은 다음과 같다.
- 가중치를 기준으로 간선을 내림차순 정렬
- 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거
- 두 정점을 연결하는 다른 경로가 없을 경우 간선을 제거하지 않음
- 간선의 수가 정점의 수보다 하나 적을 때 MST 완성
자료
- 윤성우의 열혈 자료구조 (윤성우 저, 2023.10)
'[컴퓨터 과학자 스터디] > 자료구조' 카테고리의 다른 글
| 테이블(Table)과 해쉬(Hash) (2) | 2024.12.05 |
|---|---|
| 탐색(Search) 2 (0) | 2024.12.02 |
| 탐색(Search) 1 (1) | 2024.12.02 |
| 정렬(Sorting) (0) | 2024.11.27 |
| 우선순위 큐(Priority Queue)와 힙(Heap) (0) | 2024.11.24 |
블로그의 정보
프리니의 코드저장소
Frinee